Elliptic curves: scalar multiplication revisited
Applying the scalar multiplication to points on elliptic curves over finite fields works the same way as over real numbers. The difference is that over a finite field, the operation can actually be – and it is – used for some real-world cryptography. If we look at the operation in detail, we also find some interesting features which may help or complicate things a bit when it comes to implementing such cryptography. This week we show how it works.
Elliptic curve over a finite field generates only a finite number of rational points. For example the elliptic curve we are using in this series $y^2=x^3-2x+2$ over $\mathrm{GF}(23)$ generates 32 rational points – including the point at infinity. If we pick one of these points and start adding it to itself, we can perform scalar multiplication as over real numbers[1]. But over a finite field, we reach the point at infinity at some point.
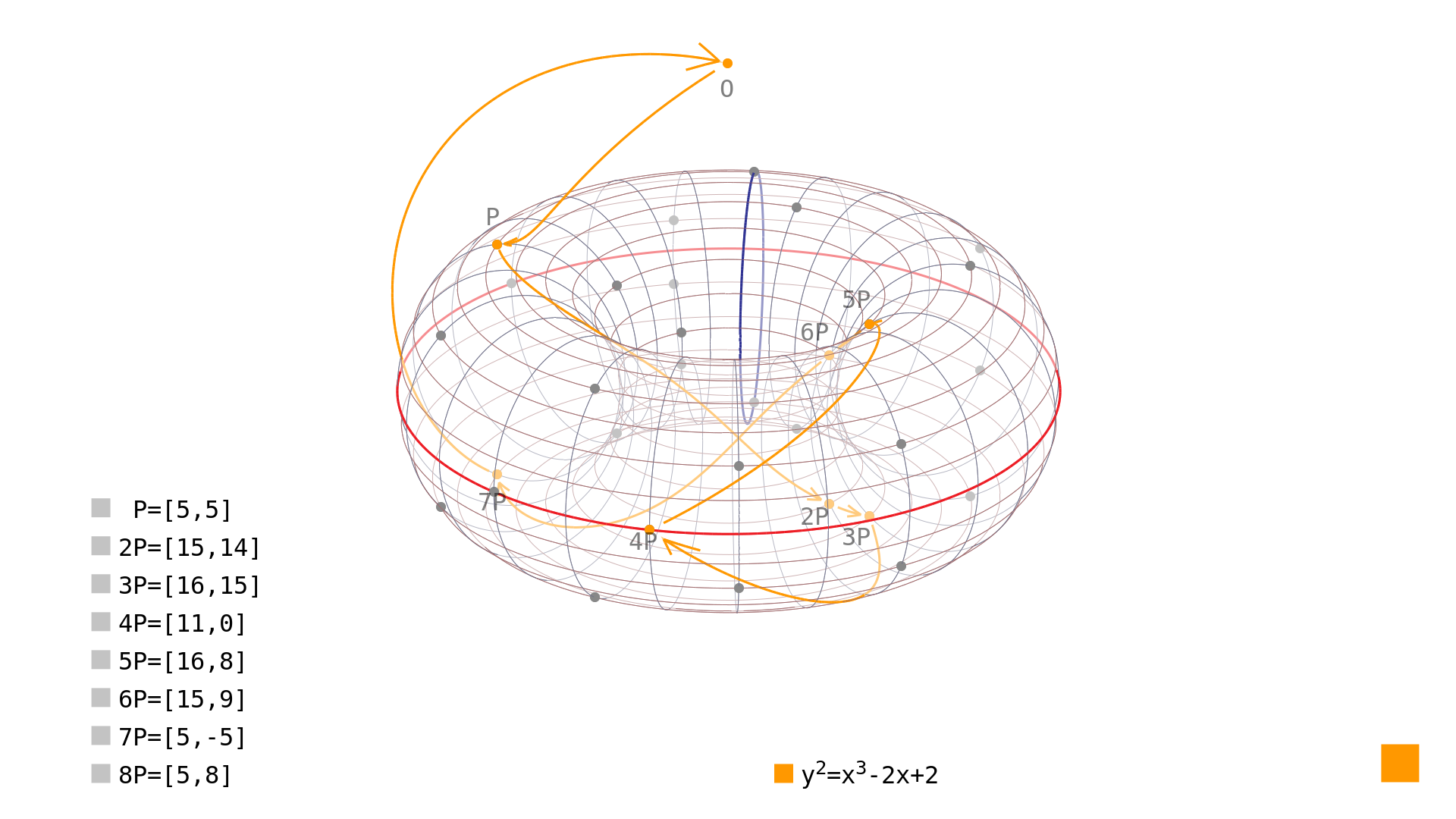
And when we continue adding the original point we started with, we see, that the points form a closed cycle. Take $P=[5,5]$ as an example:
$P=[5,5]$
$2P=P+P=[15,14]$
$3P=2P+P=[16,15]$
$4P=3P+P=[11,0]$
$5P=4P+P=[16,8]$
$6P=5P+P=[15,9]$
$7P=6P+P=[5,18]$
$8P=7P+P=O$
$9P=8P+P=P$
The cyclic nature of the group[2] (that is how is this structure called and we will return to it later on) generated by the point $P=[5,5]$ is now evident. The whole process is better illustrated in Video 1.
Video 1: Scalar multiplication – adding point $P=[5,5]$ repeatedly to itself on elliptic curve $y^2=x^3-2x+2$ over $\mathrm{GF}(23)$
To describe the nature of this cycle, we can say that the point $P=[5,5]$ on given elliptic curve over given finite field is of order 8. Or that its point order is 8. That is just a different way of saying the point generates 8 points of the underlying curve by adding it repeatedly to itself.
Another order we can study is the order of the curve. As mentioned above, our curve generates 32 rational points including the point at infinity over given finite field. We can rephrase that the order of given curve over given finite field is 32. The situation can be easily seen in Picture 1 where the points generated by $P=[5,5]$ are shown in orange and other points remain gray.
Picture 1: curve order of $y^2=x^3-2x+2$ over $\mathrm{GF}(23)$ is 32, yet the point order of $P=[5,5]$ is only 8.
We also see that the if we would want to use point this elliptic curve over given finite field for basically anything, we are unable to easily use all its points for our application. This is quite important problem which we should solve before we venture on to actually showing some real-world cryptography.
Truth is that for any elliptic curve over any finite field, it should have a prime number of points if we want to use it for something serious. That is because without adhering to this requirement, some points are of very low order and certain mathematical problems that make elliptic curve cryptography secure are actually pretty easy to crack then. Of course the other solution – finding points of reasonably high order – is also valid as we may see in one very special case. But that is far far away right now.
I can only hope this did not scare you from reading on. Rest assured we will make our curves to be the right order before we try to use them for some serious cryptography. You can read exactly about that next week!
References
1. https://trustica.cz/en/2018/04/12/elliptic-curves-multiplication-by-scalar/
2. Wikipedia contributors. (2018, March 20). Group (mathematics). In Wikipedia, The Free Encyclopedia. Retrieved 19:10, April 18, 2018, from https://en.wikipedia.org/w/index.php?title=Group_(mathematics)&oldid=831501977