Elliptic curves: prime-order curves
As we have shown last time, just mapping elliptic curve in simple Weierstrass form over a finite field does not make the curve automatically practical for cryptography. Using just a few points from the whole set cannot be very secure. Today we present two important properties the curve must possess in order to be of some practical use.
If you are here just to see the video, you can jump straight to it.
The points of the curve form a group structure[1] with point addition being the group operation. The abstraction layer of introducing scalar multiplication allows us to think and work more efficiently with this group structure. But as we have seen before[2], 32 points of the curve (including the point at infinity) does not ensure that we go through all of the points just by repeatedly adding the starting point to itself.
This comes from the fact, that the 32 is not a prime number and therefore rather sooner than later you have to end up in the point at infinity. We say, that each point might generate a different subgroup[3] from the underlying set of rational points. And it is also the case, that you can always see subgroups of various sizes in this case. Subgroup sizes are always a factor of the curve order (that is the number of rational points plus the point at infinity) or products of such factors. So for the elliptic curve we were using so far – $y^2=x^3-2x+2$ over $\mathrm{GF}(23)$ with 32 points, we have the following subgroup sizes and points which generate subgroups of such sizes:
| Order | Points |
|---|---|
| 2 | $[0,18]$, $[0,5]$, $[11,0]$, $[9,0]$, $[3,0]$ |
| 4 | $[7,20]$, $[15,14]$, $[15,9]$, $[7,3]$ |
| 8 | $[12,21]$, $[5,18]$, $[16,15]$, $[4,14]$, $[4,9]$, $[16,8]$, $[5,5]$, $[12,2]$ |
| 16 | $[1,22]$, $[20,21]$, $[14,21]$, $[10,19]$, $[18,18]$, $[22,16]$, $[2,12]$, $[2,11]$, $[22,7]$, $[18,5]$, $[10,4]$, $[20,2]$, $[14,2]$, $[1,1]$ |
Table 1: Subgroup sizes (point orders) for all rational points of the curve $y^2=x^3-2x+2$ over $\mathrm{GF}(23)$
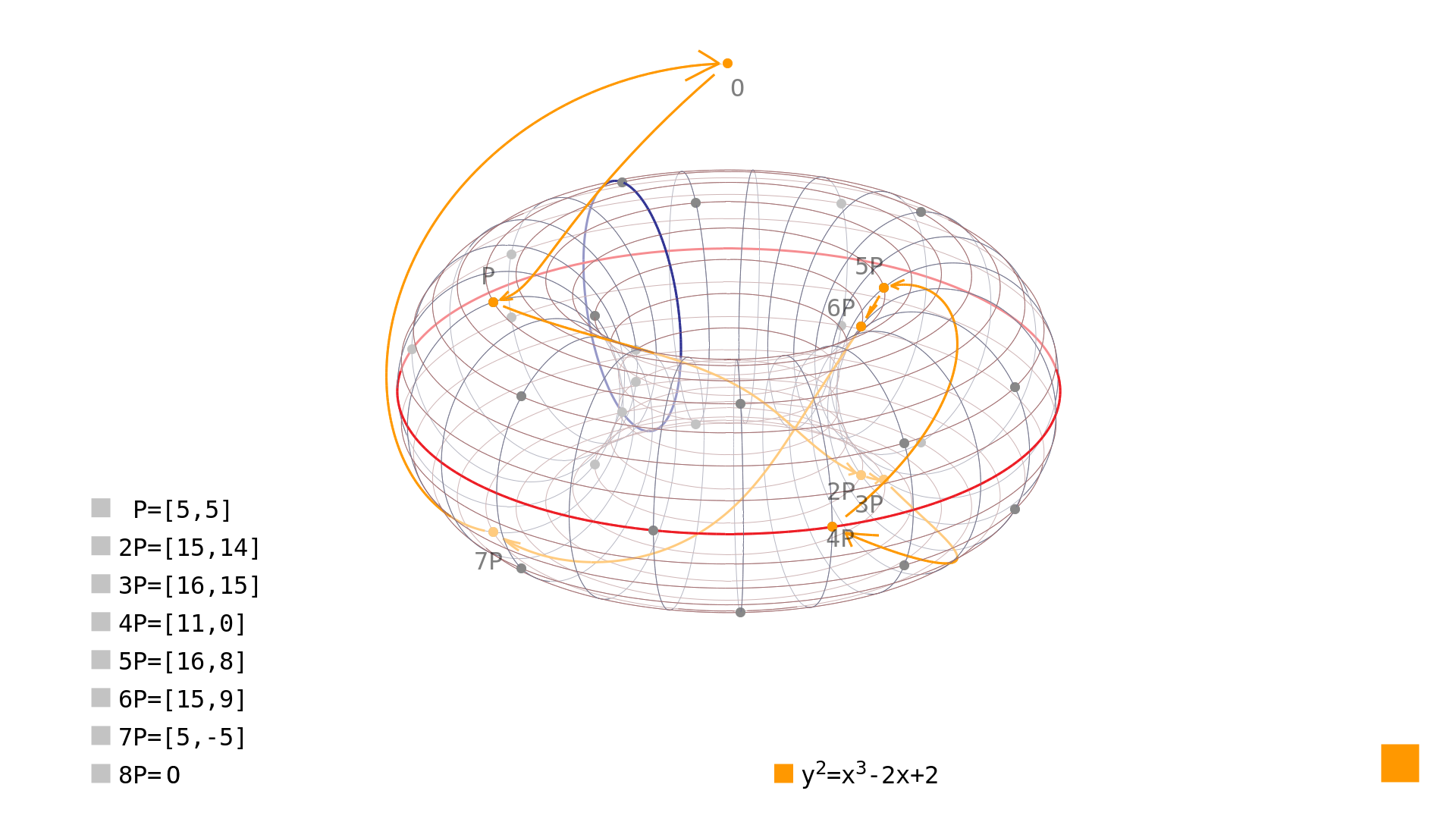
As the curve order is the number of rational points plus one (for the point at infinity), the point order is the number of the rational points generated by repeatedly adding a point to itself – including the point at infinity. The group presented in the previous article[2] can be seen in Picture 1.
Picture 1: subgroup of size 8 generated by point $P=[5,5]$ on the elliptic curve $y^2=x^3-2x+2$ over $\mathrm{GF}(23)$
To overcome this limitation, we simply choose coefficients $a$ and $b$ to ensure that the number of rational points over given finite field plus the point at infinity is a prime number. In our case, just a little tweak would do the job:
$y^2=x^3-2x+6$
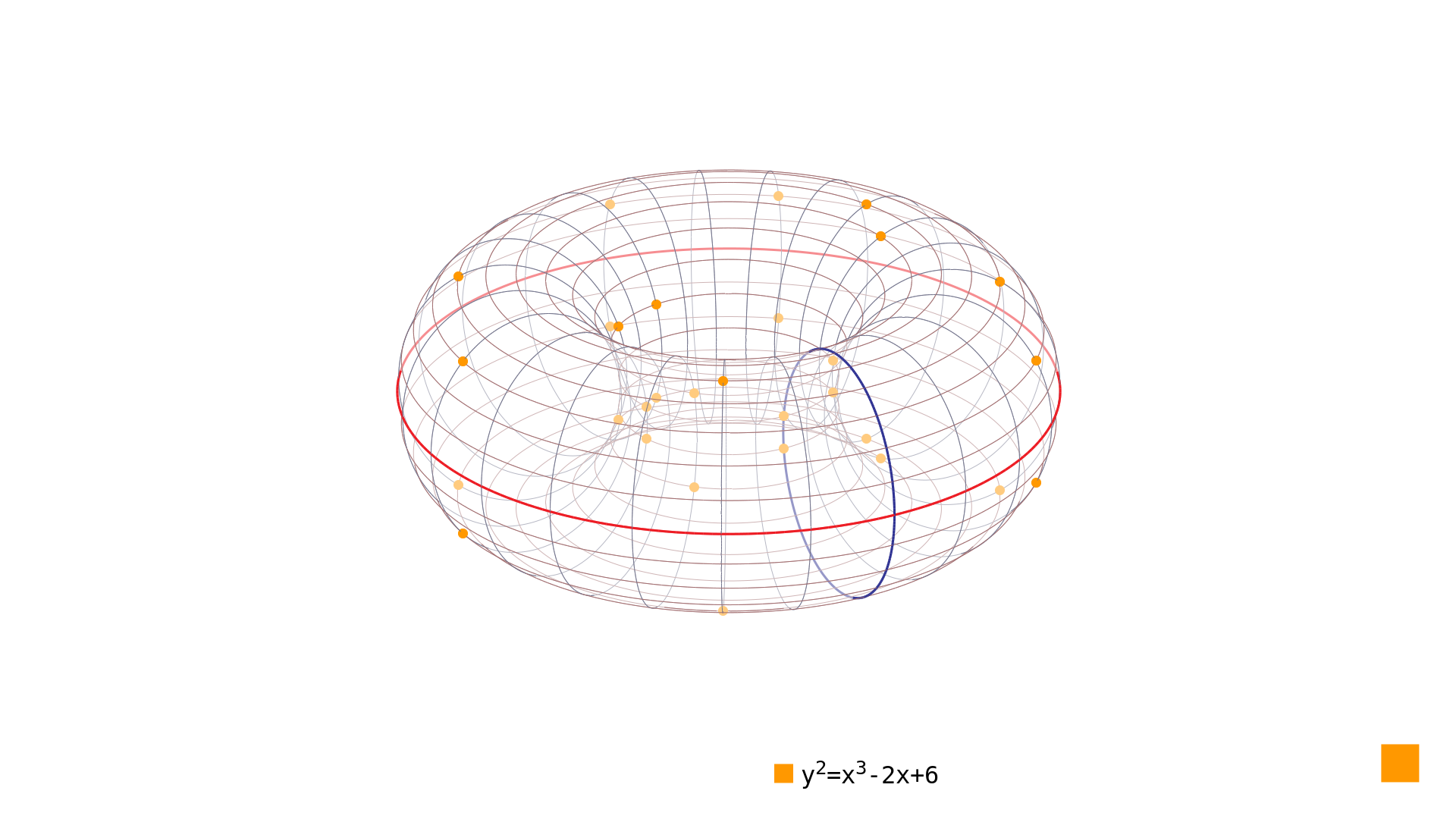
The order of this nice little curve is 31 – that is 30 rational points and the point at infinity as can be seen in Picture 2.
Picture 2: prime-order elliptic curve $y^2=x^3-2x+6$ over $\mathrm{GF}(23)$
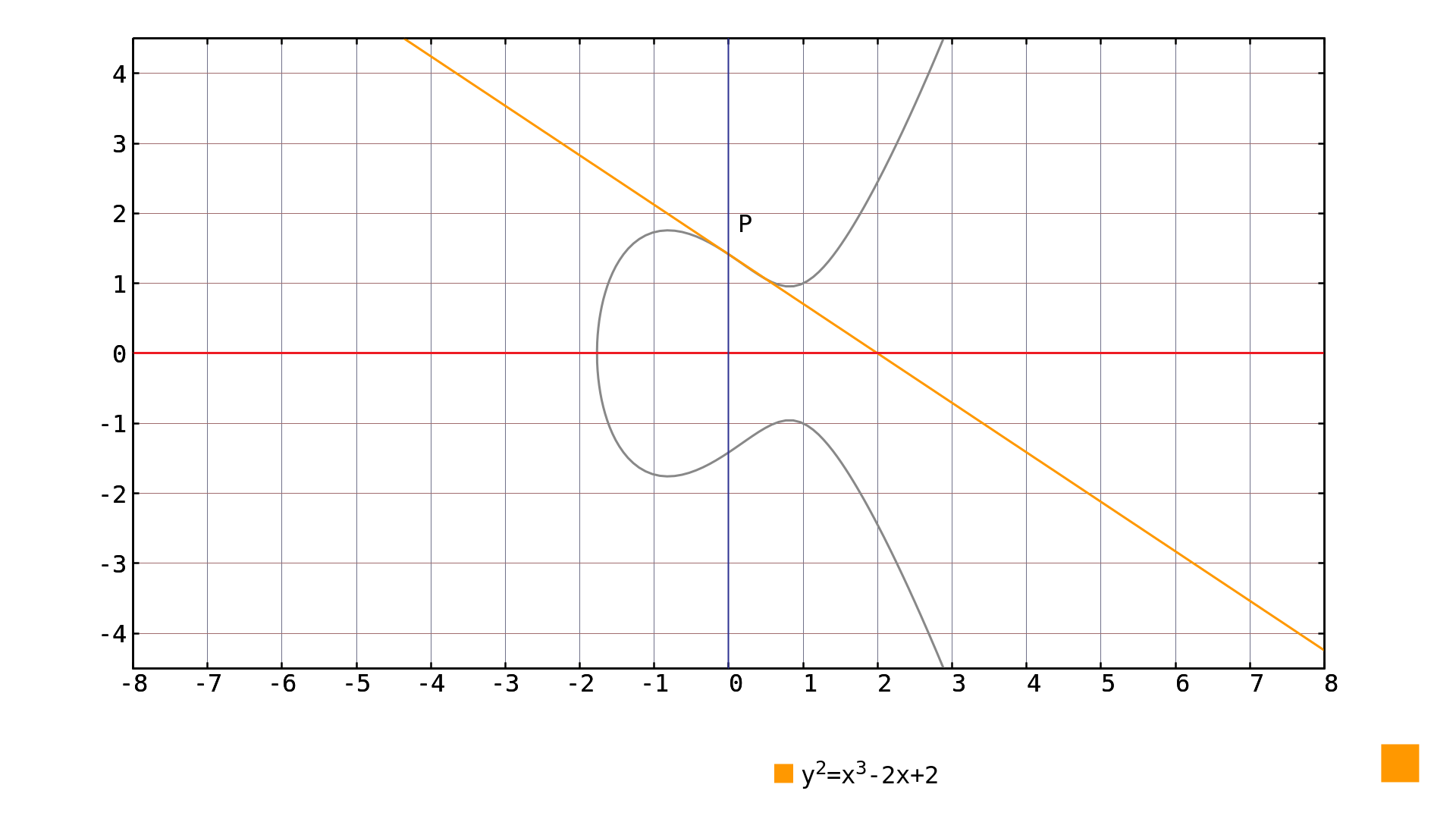
If we look at Picture 2 closely, we see that there are two points with $x=0$. Problem is, that we cannot use these points as our starting points to generate all points of the curve. Remember the point doubling operation[4] and look at the slope of the tangent (over real numbers) at point $x=0$ in Picture 3:
Picture 3: inflection point
Although the tangent is defined there, it does not cross any other point of the elliptic curve. Therefore once again, the double of such point is the point at infinity. The problem expresses itself over $\mathrm{GF}(p)$ as well and the tangent line does not cross any other rational point.
Next problem would be points with $y=0$ where it would be impossible to calculate the slope of the tangent as:
$d=\frac{3x+a}{2y}$
As you can easily see, this would turn into:
$d=\frac{3x+a}{0}$
Good luck with computing that – to state it lightly. But there is also another problem. We cannot just omit the points with $x=0$ or $y=0$ while traversing over the points of the curve. We will hit them eventually and although we might (and mostly we will) generate all points of given curve over given finite field, the group law would fail at these points as we are unable to double them.
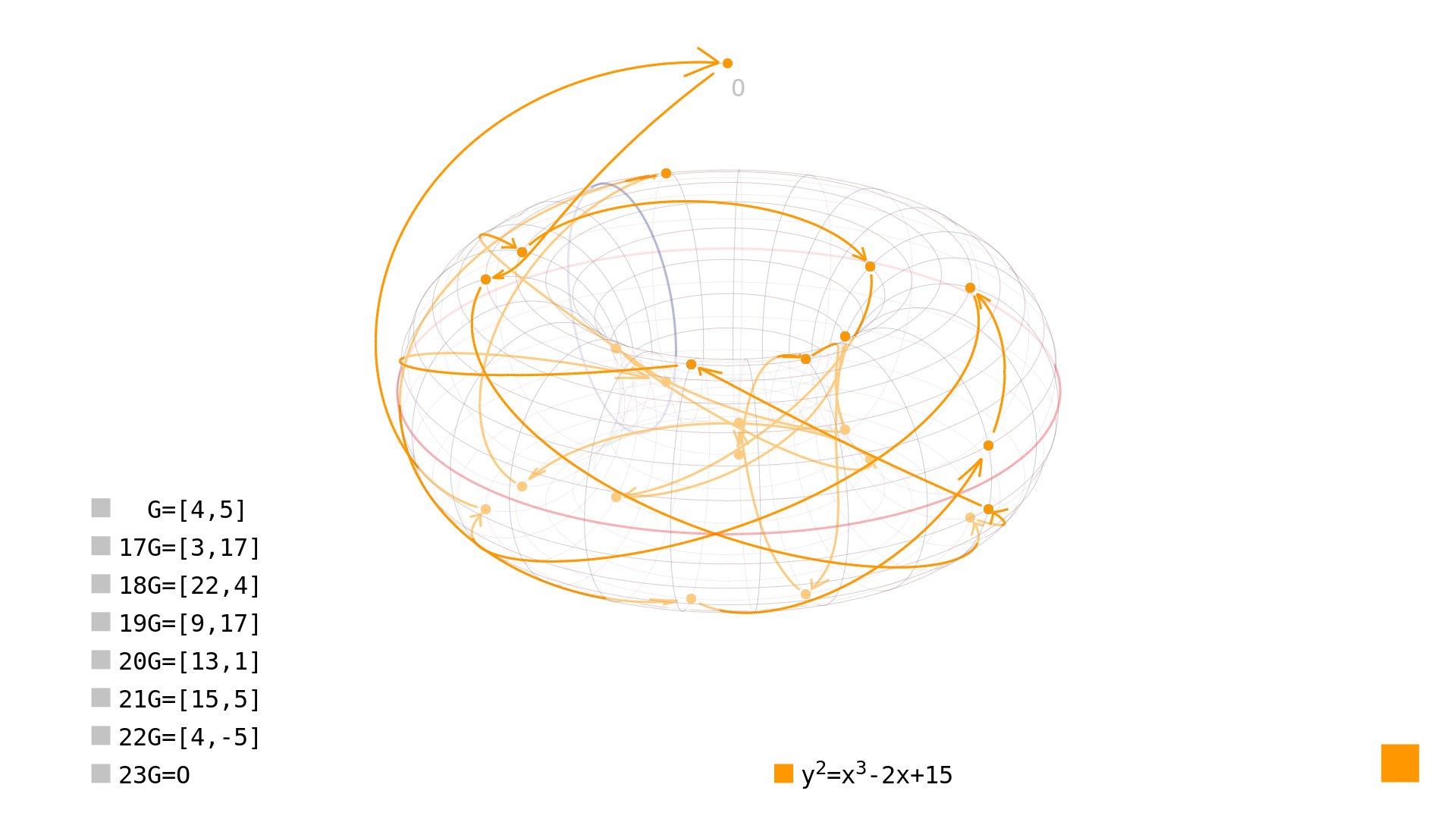
Therefore we need to choose coefficients $a$ and $b$ not only to generate a prime-order curve, but also a curve without any points on the X or Y axes. So we tweak our current curve even more and see that $y^2=x^3-2x+15$ over $\mathrm{GF}(23)$ is The Curve for our purpose. Watch the traversal of its points in Video 1 below.
Video 1: Prime-order curve $y^2=x^3-2x+15$ over $\mathrm{GF}(23)$ with no points on the X and Y axes.
This curve forms a group without subgroups, the group law applies without exceptions and therefore any point can be chosen to be a generator for curve points. This curve can be used for some practical – although very weak because of its size – cryptography. You can see the group structure in Picture 4.
Picture 4: Group structure of the elliptic curve $y^2=x^3-2x+15$ over $\mathrm{GF}(23)$.
And that is all for today. Thank you you made it this far!
Now we are nearing the end of our series where we should discover how to use all of this for some practical cryptography and eventually secure our online communication. Next week we are about to witness a major speedup of the scalar multiplication algorithm. Remember to subscribe to our YouTube channel and follow us on Twitter. See ya next Thursday!
References
1. Wikipedia contributors. (2018, April 20). Group (mathematics). In Wikipedia, The Free Encyclopedia. Retrieved 11:54, April 25, 2018, from https://en.wikipedia.org/w/index.php?title=Group_(mathematics)&oldid=837324573
2. https://trustica.cz/en/2018/04/19/elliptic-curves-scalar-multiplication2/
3. Wikipedia contributors. (2018, February 12). Subgroup. In Wikipedia, The Free Encyclopedia. Retrieved 11:55, April 25, 2018, from https://en.wikipedia.org/w/index.php?title=Subgroup&oldid=825271227
4. https://trustica.cz/en/2018/03/22/elliptic-curves-point-doubling/