Elliptic curves: point addition
Another week, another point operation on elliptic curves. This time we are about to explore a simple point addition of two different points on elliptic curve in simple Weierstrass form. Although there are still some possibilities of enhancing the visualizations, our focus is now on finishing this series to a point where we can show at least Diffie-Hellman key exchange[1].
In previous articles we covered transformation of elliptic curve in generic Weierstrass form to simple Weierstrass form[2], mapped this curve onto finite field of prime size and shown the set of rational points the elliptic curve forms over such prime field[3] and finally shown the first point operation – the negation[4]. That operation alone is not actually useful – yet – but it has to be explained first as we will use it in our explanation of point addition.
We continue to use our familiar elliptic curve in simple Weierstrass form:
$y^2=x^3+ax+b$
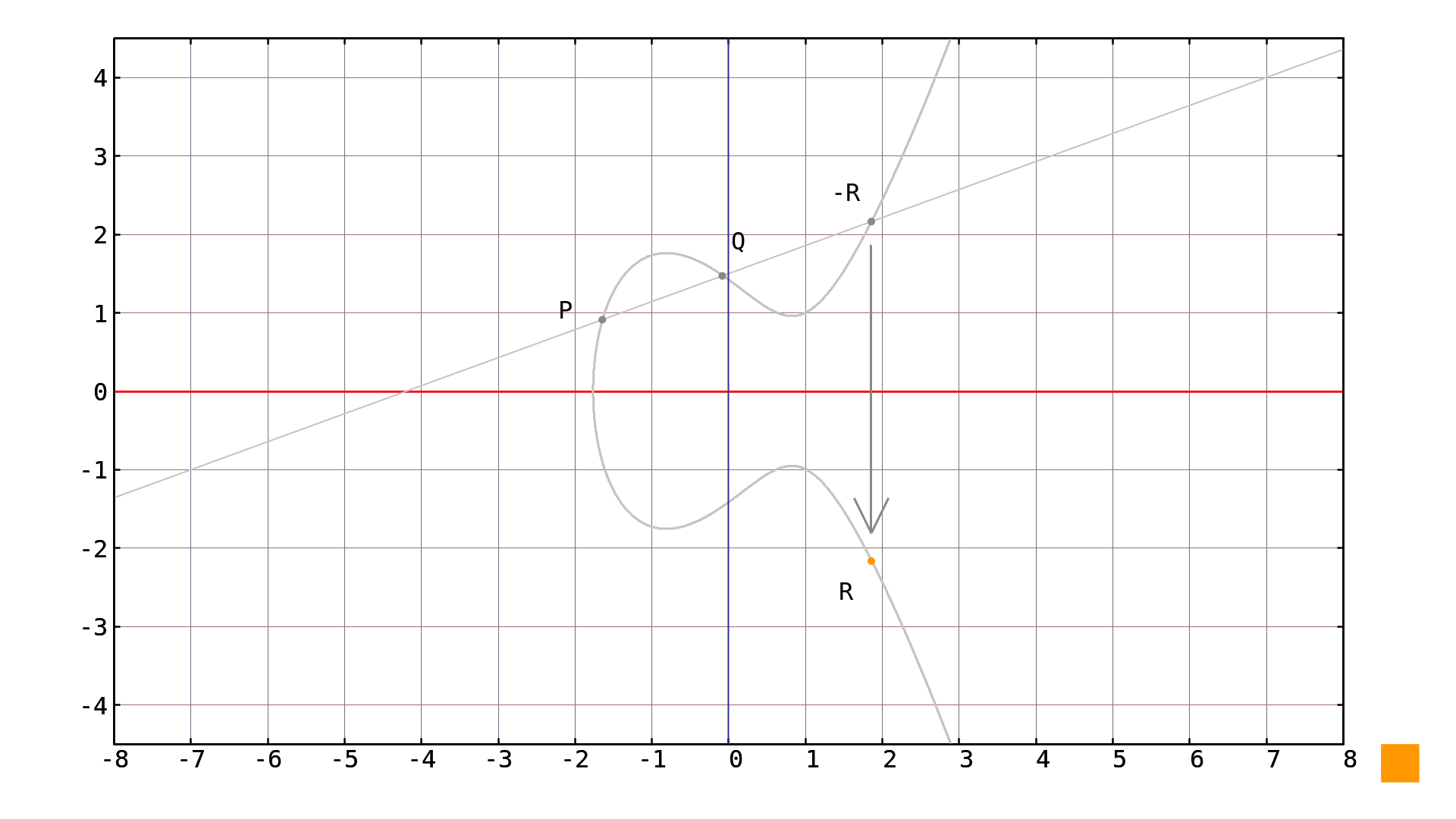
To sum two points P and Q lying on the elliptic curve, we draw a straight line going through both of them and the third point where this line intersects the elliptic curve is the negation of the result. Using the point negation explained in previous article we get the resulting point. Everything can be easily understood looking at Picture 1 depicting the operation graphically.
Picture 1: Point addition $R=P+Q$ of points $P\approx[-2.13,1.05]$ and $Q\approx[-0.12,1.93]$ on the elliptic curve in simple Weierstrass form $y^2=x^3-2x+2$ over $\mathbb{R}$.
In the following text (and upcoming articles), we will use the $P=[P_x,P_y]$ notation. This might look unfamiliar but it resembles more the eventual programmatic notation in object-oriented languages like „p->x“ or „p.x“ and also we want to highlight which point we are working with. Remember, there are just two coordinates $x$ and $y$ but there will be more points to come as we go through more complex operations.
Graphically, this operation does not look bad at all. But we want to calculate everything and not just draw a nice picture. We start with the equation of the line going through points $P$ and $Q$. As any other line equation, we can write it as:
$y=dx+e$
Where $d$ is called „slope“ of the line and $e$ you can imagine as offset from the X axis (that is from $y=0$). Calculating the slope is pretty easy as well:
$d=\frac{Q_y-P_y}{Q_x-P_x}$
The offset $e$ can be obtained from either of points. Using the point $P$, it is:
$e=P_y-dP_x$
Now we have equations of two two-dimensional objects in the real plane and want to find their intersections. Nothing can be easier, we just need to find points which satisfy both equations. And in this case we can merge the two equations into one:
$(dx+e)^2=x^3+ax+b$
And rewrite it in straightforward polynomial form:
$x^3-d^2x^2+(a-2de)x+b-e^2=0$
This is actually cubic equation, that might look hard to solve. But remember – we are trying to find the third intersecting point and we already know two. And x-coordinates of those two points are also roots of this polynomial. Therefore we can simplify this equation in two steps. Firstly we divide it by the polynomial $(x-P_x)$:
$x^2+(P_x-d^2)x+a-2de+P_x^2-P_xd^2=0$
We see that we have reduced the cubic to rather simple quadratic equation, which can be solved by anyone with high school education. But we know we can simplify it even more by dividing this intermediate result by the polynomial $(x-Q_x)$:
$x+P_x-d^2+Q_x=0$
With this linear equation at hand, we can easily get the x-coordinate of the points $-R$ and therefore $R$:
$R_x=d^2-P_x-Q_x$
Calculating the y-coordinate of the result is as simple as putting our x-coordinate into the equation of the intersecting line and – because $R_y=-(-R)_y$ – negating it:
$R_y=-P_y-d(R_x-P_x)$
The situation is – at least graphically – quite similar when dealing with elliptic curves over a finite field. You can see the beautiful torus with the same operation depicted in Picture 2.
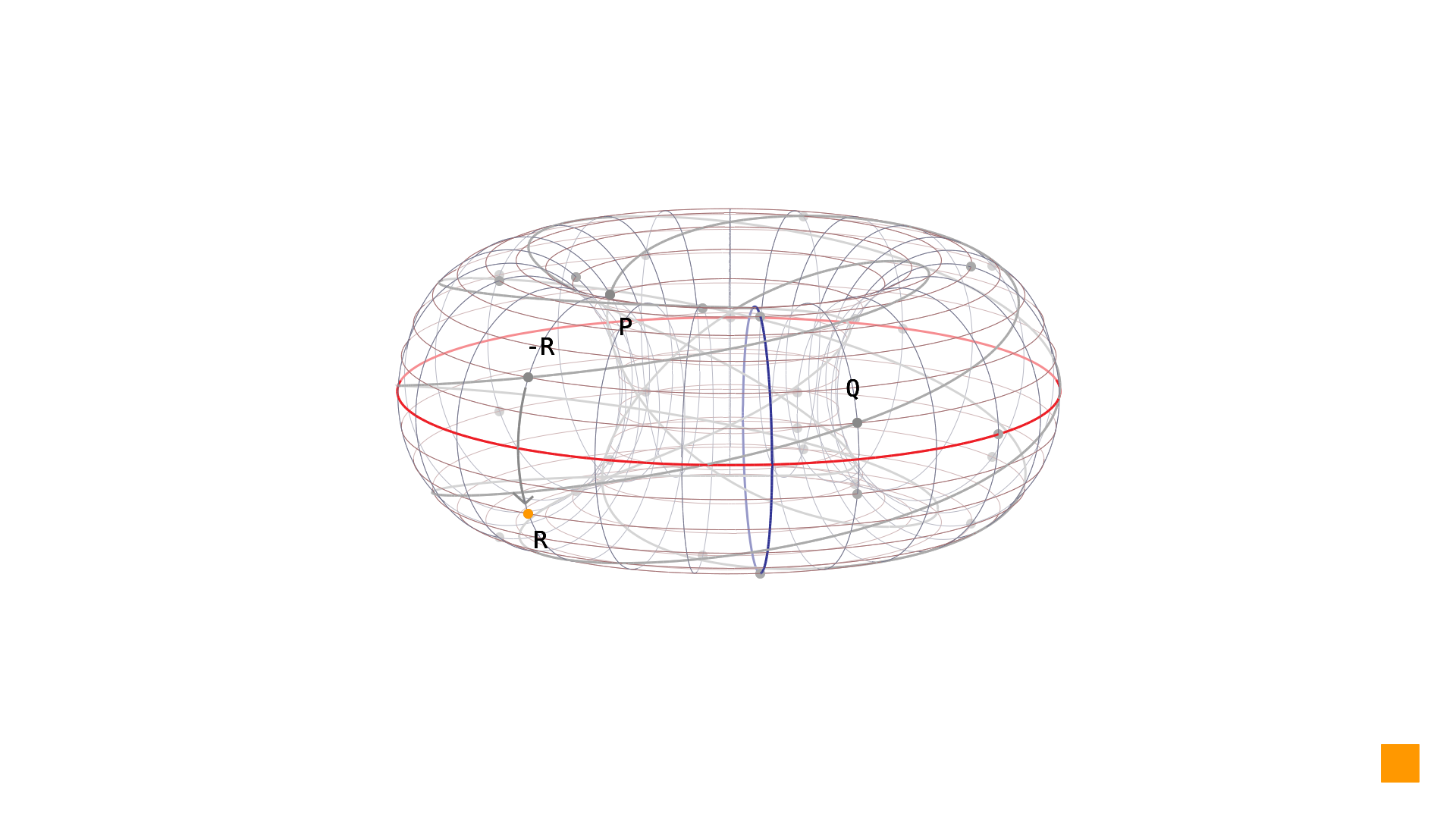
Picture 2: Point addition $R=P+Q$ of points $P=[15,9]$ and $Q=[1,1]$ on the elliptic curve in simple Weierstrass form $y^2=x^3-2x+2$ over $\mathrm{GF}(p)$.
The visualization of this operation as a static picture is still relatively hard to grasp, therefore I can only suggest looking at the Video 1 below which shows animations of the operation both over $\mathbb{R}$ and $\mathrm{GF}(p)$.
Video 1: Point addition $R=P+Q$ of points $P\approx[-2.13,1.05]$ and $Q\approx[0.12,1.93]$ on the elliptic curve in simple Weierstrass form $y^2=x^3-2x+2$ over $\mathbb{R}$ and of points $P=[15,9]$ and $Q=[1,1]$ over $\mathrm{GF}(p)$..
To achieve the same results over a finite field, we use the same equations we have derived above, but when it comes to calculating the slant value, we cannot do a regular division but rather we have to use „multiplicative inverse“ operation of the finite field to get the actual usable value. If there is time (and readers‘ interest) we may tackle that in the future as well.
You may wonder, why the summation of points works this way – that is definitely a valid question which will (hopefully) be answered in one of my upcoming articles. A short explanation is that we need to define the operation in a way that helps us creating a „group structure“ of the points on the curve.
I hope you still do enjoy our route into the depths of elliptic curve cryptography. Rest assured it will be a long roller-coaster ride if you stay tuned and eventually we might actually get to securing the online communication. See you next week!
References
1. Wikipedia contributors. (2017, December 17). Weierstrass’s elliptic functions. In Wikipedia, The Free Encyclopedia. Retrieved 11:43, March 6, 2018, from https://en.wikipedia.org/w/index.php?title=Weierstrass%27s_elliptic_functions&oldid=815834613#General_theory
2. https://trustica.cz/en/2018/02/22/introduction-to-elliptic-curves/
3. https://trustica.cz/en/2018/03/01/elliptic-curves-over-finite-fields/
4. https://trustica.cz/en/2018/03/08/elliptic-curves-point-negation/