Elliptic Curve Digital Signature Algorithm
After slightly going astray from the elliptically curved path on our favorite doughnuts, we return from the realm of electronic mail to much more interesting world of mathematics. Today, our effort to explain elliptic curves in simple Weierstrass form and their usage should reach its second culmination. With Diffie-Hellman key exchange explained, the only part that is missing is some digital signature scheme. So please read on to find the beauty of the Elliptic Curve Digital Signature Algorithm beast.
If you think you can grasp it all at once and you just want to see the video, here it is – but you have been warned!
Digital signatures pose an unique challenge to implement properly. The Elliptic Curve Diffie-Hellman key exchange[1] was rather easy. But this time you need a mechanism with two parts: the signature creation and signature verification. These two parts need to be tied closely together, yet have to function separately.
Creating and verifying digital signatures using elliptic curves in simple Weierstrass form[2] if usually achieved by implementing a variant of Schnorr’s signature[3] – the core idea behind the Digital Signature Algorithm[4] (DSA for short). The Elliptic Curve DSA[5] (ECDSA) is the signature scheme we describe in this article and show you a practical example of usage.
Once again, there are two parties willing to communicate, conveniently named Alice and Bob. We designate Alice to be the one creating the digital signature and Bob to do the verification. This allows us to easily describe both processes.
Signature creation
As with ECDH, the two parties must agree upon the curve to be used and the generator point. The curve and the generator Alice and Bob has agreed upon can be seen in Picture 1. It is our well-known curve we have designed throughout this series: $y^2\equiv x^3-2x+15~\mathrm{mod}~23$ and the generator $G=[4,5]$.
Picture 1: The elliptic curve in simple Weierstrass form $y^2=x^3-2x+15$ over $\mathrm{GF}(23)$ and the generator $G=[4,5]$.
Alice – as the one doing the signing – chooses a random number to be her private key. Of course, she must keep the private key secret. By multiplying the generator by her private key, she obtains her public point which she can send to Bob. In our example, we use the same private key as when explaining ECDH – $a=3$.
$A=a\cdot G$
$A=3\cdot[4,5]$
$A=[13,22]$
To make sure Bob can verify the signature, Alice has to make sure he knows her public key. Typically a personal meeting is the best option for exchanging public keys and afterwards you can just start using them. If that is not possible, it is always an option to send them for example via email and verify at least the hash of the key over a phone. That way you can at least guess if the person you are talking to is really the one you know.
The signature algorithm does not sign the whole message, rather it signs a $n$-bit hash value of the message contents. So before Alice starts signing, she has to calculate the hash value of the message contents and use $n$ bits from this value as the actual digest $z$ to be signed. While using the curve the parties have agreed upon, we can come up for example with:
$N=23$
$2^4<23<2^5$
$n=5$
$z=10$
Our elliptic curve has 23 points – the 22 rational points and the point $O$ at infinity. Therefore its order is $N=23$ and the bit-size of such number is $n=5$. The message digest of $z=10$ is a suitable value to sign.
Creating the digital signature using the ECDSA scheme starts with choosing a random number $k$ between 1 and $N$. The point $K$ is then computed by multiplying the generator by the number $k$. In our example we choose a random number:
$k=19$
$K=k\cdot G$
$K=19\cdot[4,5]$
$K=[9,17]$
The X-coordinate of this point $K$ is the first half of the signature, usually labeled $r$. In our case:
$r=9$
The other half of the signature is calculated using some relatively easy modular arithmetic. Explaining why this works and giving a formal proof is beyond the scope of this article, but maybe we will tackle that in the future. The second half is usually labeled $s$ and can be calculated as:
$s=\frac{z+ra}{k}~\mathrm{mod}~N$
It looks rather complicated, but if we split it up to smaller pieces, it is relatively trivial to compute. The calculation for our example is as follows:
$s=k^{-1}\cdot(z+ra)~\mathrm{mod}~N$
$s=19^{-1}\cdot(10+9\cdot 3)~\mathrm{mod}~23$
$19^{-1}~\mathrm{mod}~23=17\quad\iff\quad 19\cdot 17~\mathrm{mod}~23=1$
$10+9\cdot 3~\mathrm{mod}~23=14$
$s=17\cdot 14~\mathrm{mod}~23$
$s=8$
So for our example we have come to the pair of numbers $(r,s)=(9,8)$ to be Alice’s signature of the message with digest $z=10$.
Signature verification
Before actually trying to verify the signature, it is important to calculate the same digest value of the incoming message. In our example we can safely assume that Bob has computed the same digest $z=10$.
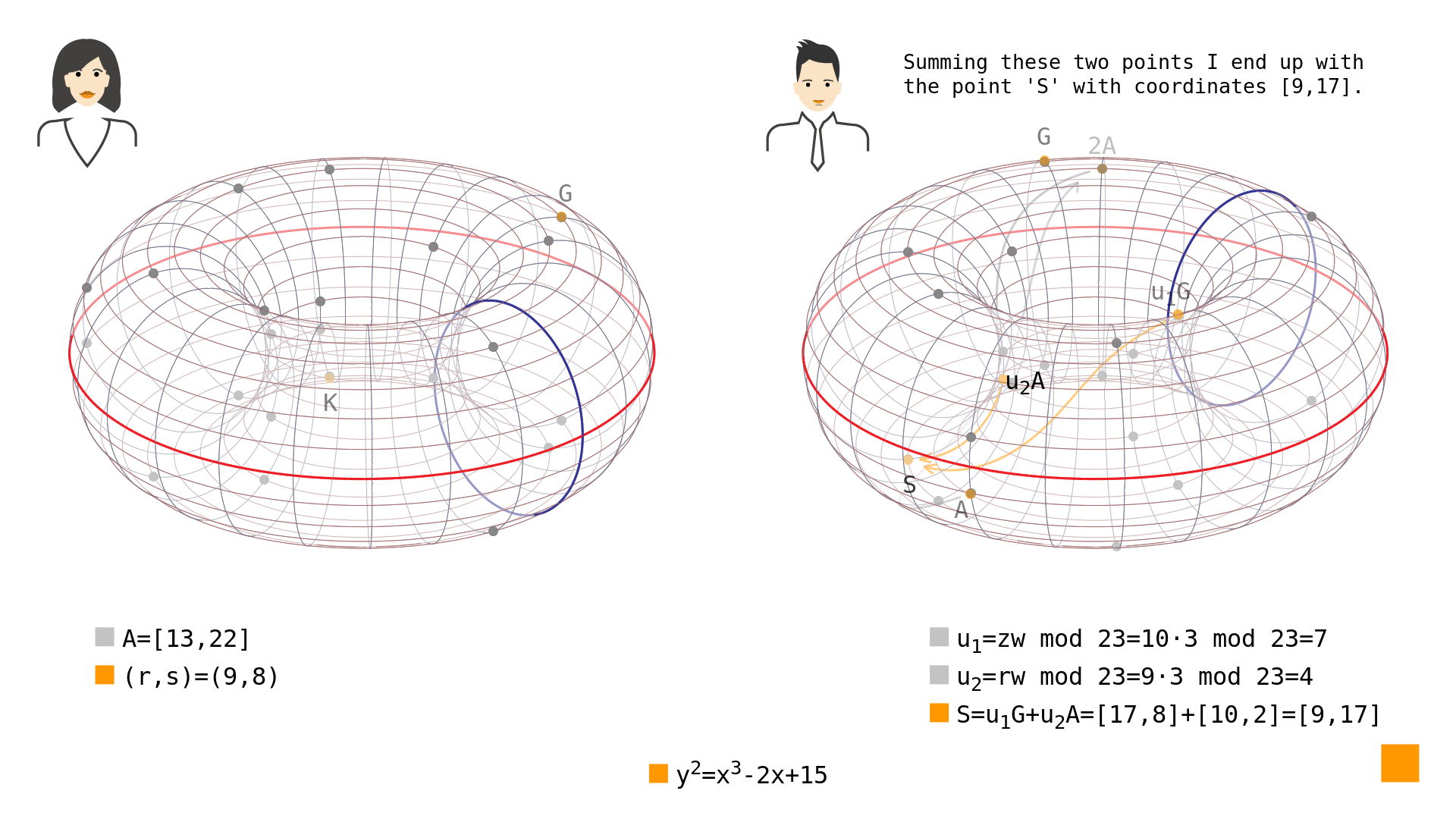
Once again the proof of the following mathematics is beyond the scope of this article, but using it is straightforward. Bob computes $w$ – the multiplicative inverse of $s$ modulo $N$ and then he computes two coefficients $u_1$ and $u_2$ which are needed for computing the point signature verification point $S$ from the generator $G$ and Alice’s public point $A$:
$w=s^{-1}~\mathrm{mod}~N$
$u_1=zw~\mathrm{mod}~N$
$u_2=rw~\mathrm{mod}~N$
Using the numbers from our example, we see that Bob comes to following coefficients:
$w=8^{-1}~\mathrm{mod}~23$
$w=3\quad\iff\quad 3\cdot8~\mathrm{mod}~23=1$
$u_1=10\cdot 3~\mathrm{mod}~23$
$u_1=7$
$u_2=9\cdot 3~\mathrm{mod}~23$
$u_2=4$
With these coefficients at hand it is possible to calculate the signature verification point $S$ using the following procedure:
$S=u_1G+u_2A$
Back to our example, we see that the signature verification point Bob calculates is as follows:
$u_1G=7\cdot[4,5]$
$u_1G=[17,8]$
$u_2A=4\cdot[13,22]$
$u_2A=[10,12]$
$S=[13,22]+[10,12]$
$S=[9,17]$
You can see the intermediate points and the result in Picture 2.
Picture 2: Calculating the point $S=[9,17]$ from points $u_1G=[17,8]$ and $u_2A=[10,12]$ on elliptic curve in simple Weierstrass form $y^2=x^3-2x+15$ over $\mathrm{GF}(23)$
To verify the signature, all we need is to compare the value $r$ to the X-coordinate of the signature verification point $S$.
$r=S_x\Rightarrow$ signature is valid
As we see in our example, $r=9$ and $S_x=9$, therefore Bob is able to successfully verify the Alice’s signature of message with digest $z=10$ by using the signature $(r,s)=(9,8)$ she sent to him and her public point $A=[13,22]$ he already knew.
The video
If you have read everything above (or you have jumped straight to the video), you can see the ECDSA signature creation and verification in Video 1. It is not as action packed as our last video about secure email communication[6], but it is definitely worth watching!
Video 1: Creating signature by Alice – known by her public point $A=[13,22]$ – of the message with digest $z=10$ on the elliptic curve in simple Weierstrass form $y^2=x^3-2x+15$ over $\mathrm{GF}(23)$ with the point $G=[4,5]$ as the generator.
Thank you for staying with us for all the 14 articles about elliptic curves in simple Weierstrass form. As you probably know, we are about to launch something and that something will be using elliptic curves – so please, subscribe to our YouTube channel, follow us on Twitter and read our weekly articles. Each and every Thursday we are here! See you next week.
References
1. https://trustica.cz/en/2018/05/17/elliptic-curve-diffie-hellman-key-exchange/
2. https://trustica.cz/en/2018/02/22/introduction-to-elliptic-curves/
3. Wikipedia contributors. (2018, January 30). Schnorr signature. In Wikipedia, The Free Encyclopedia. Retrieved 21:15, June 6, 2018, from https://en.wikipedia.org/w/index.php?title=Schnorr_signature&oldid=823175408
4. Wikipedia contributors. (2018, March 11). Digital Signature Algorithm. In Wikipedia, The Free Encyclopedia. Retrieved 21:16, June 6, 2018, from https://en.wikipedia.org/w/index.php?title=Digital_Signature_Algorithm&oldid=829976437
5. Wikipedia contributors. (2018, March 3). Elliptic Curve Digital Signature Algorithm. In Wikipedia, The Free Encyclopedia. Retrieved 21:16, June 6, 2018, from https://en.wikipedia.org/w/index.php?title=Elliptic_Curve_Digital_Signature_Algorithm&oldid=828648744
6. https://trustica.cz/en/2018/05/31/secure-email-communication/