Elliptic curves: point negation

Venturing closer to our goal of using elliptic curves for digital signatures and encryption, we describe the simplest point operation on elliptic curve in Weierstrass form. This operation is called negation and it somehow resembles the negation of numbers you learned about in elementary school. We have (sort of) finalized the software stack for visualizing elliptic curves both in 2D or 3D so I would like to hear some feedback if the pictures - and especially the video - are clear and easy to understand. And now for something completely negating...

Maybe this time we should start with a one-minute video that explains it all and then just go over the details so that anyone can easily understand. Also, I would really love to hear any feedback on how would you like to improve these visualizations. Although it is really time consuming if you want to create a decent-looking visualization of elliptic curves over a finite field, I find it definitely worth it.

Negating a point on an elliptic curve in the simple Weierstrass form[1] is relatively simple both over real numbers $\mathbb{R}$ and over a finite field $\mathrm{GF}(p)$[2]. For any point $P=[P_x,P_y]$ lying on the elliptic curve $y^2=x^3+ax+b$ its negation can be calculated as: $-P=[P_x,-P_y]$ For elliptic curve over $\mathbb{R}$ the operation is depicted in picture 1.

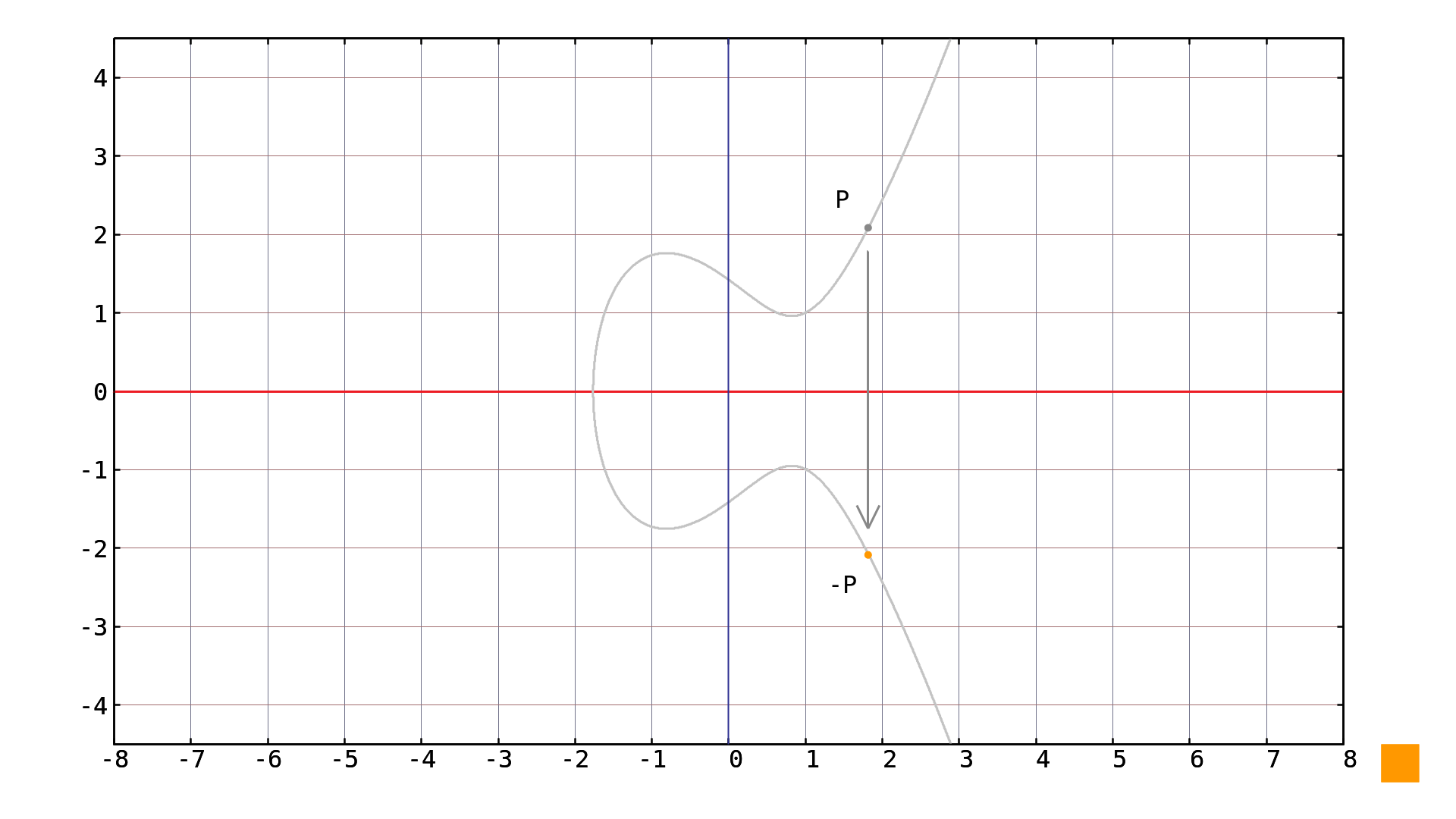
Picture 1: Negation of the point $P\approx[1.48,2.46]$ on the elliptic curve $y^2=x^3-2x+2$ Except for the special case where $y=0$ the coordinate negation over a finite field $\mathrm{GF}(p)$ must use modular arithmetic. But as this is very simple subtraction, we can calculate the resulting Y coordinate without using actual modular arithmetic by subtracting the original Y coordinate value from the size of the field: $-P_y \mod p=p-P_y$ Such negation can be seen in picture 2.

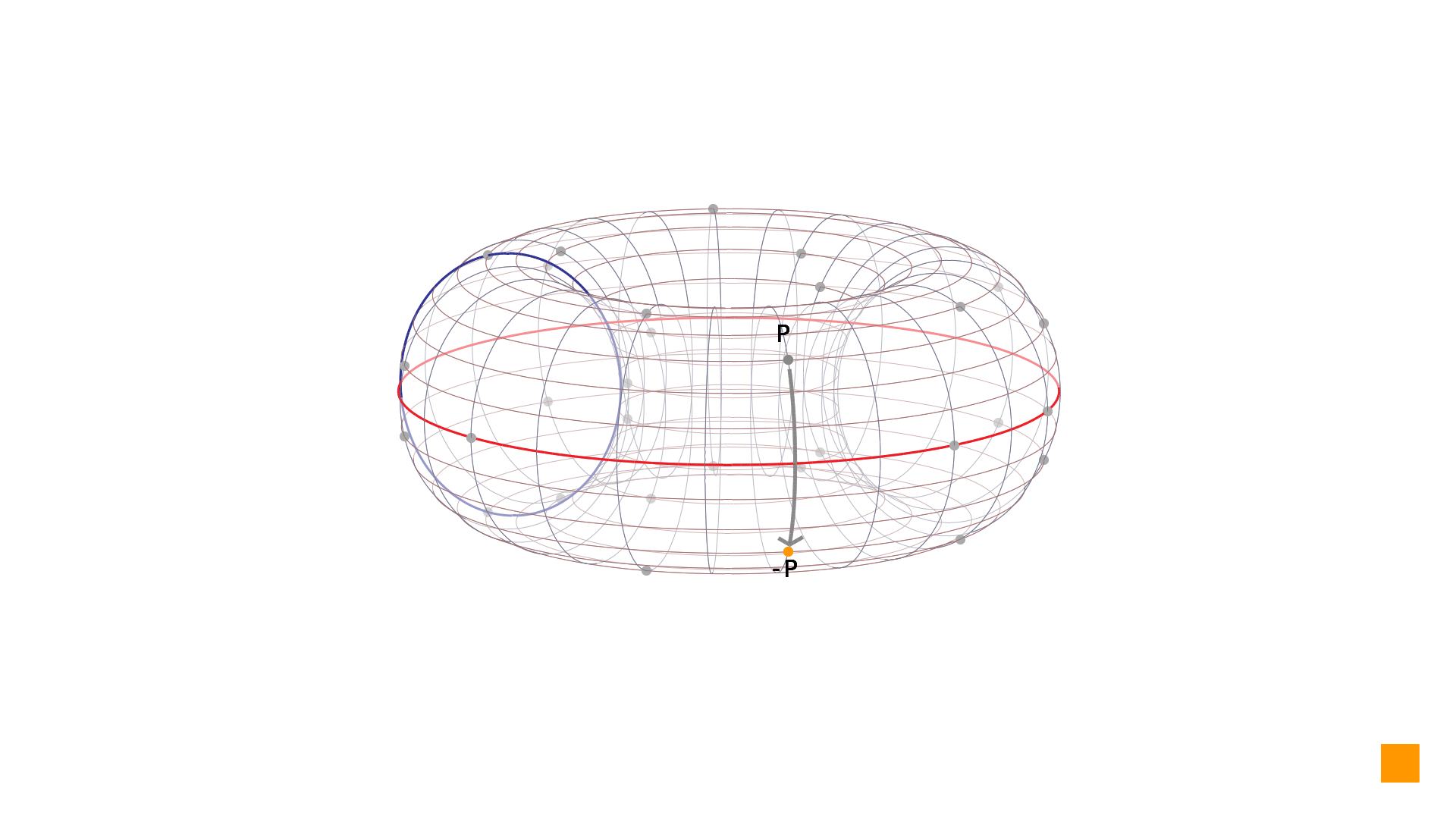
Picture 2: Negation of the point $P=[7,3]$ on the elliptic curve $y^2\equiv x^3-2x+2\mod 23$ Thank you for reading this series and not stopping when the first hint this is going to be about mathematics came. As you have probably guessed, this series paves the path for our new product for securing online communication - but the time has not come yet. Therefore, see you next week with point addition which should bring some action to these relatively static videos.

References

 1. Wikipedia contributors. (2017, December 17). Weierstrass's elliptic functions. In Wikipedia, The Free Encyclopedia. Retrieved 11:43, March 6, 2018, from https://en.wikipedia.org/w/index.php?title=Weierstrass%27s_elliptic_functions&oldid=815834613#General_theory

 2. Weisstein, Eric W. "Finite Field." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/FiniteField.html