Montgomery Curves in Projective Coordinates

If you ever wondered, how does the cryptography Cryptoucan™ actually employ look like and how do the elliptic curves used actually look, now it is time you wonder no more. Read on to see what does the curve used for encryption look like!

In the past, we covered the elliptic curve cryptography (ECC)[1] using elliptic curves in simple Weierstrass form[2] quite extensively[3]. But the truth is that Cryptoucan™ is using better elliptic curves to do the job. First elliptic curve in the list would definitely be the Montgomery curve[4] in affine[5] and projective[6] coordinates.

Montgomery curve in affine coordinates is a set of points in the two-dimensional plane satisfying the following equation: $$By^2=x^3+Ax^2+x$$ Let's pick some coefficients like $A=2$ and $B=4$ and look for yourself how does the curve look like in Picture 1. It looks pretty similar to elliptic curves in simple Weierstrass form.

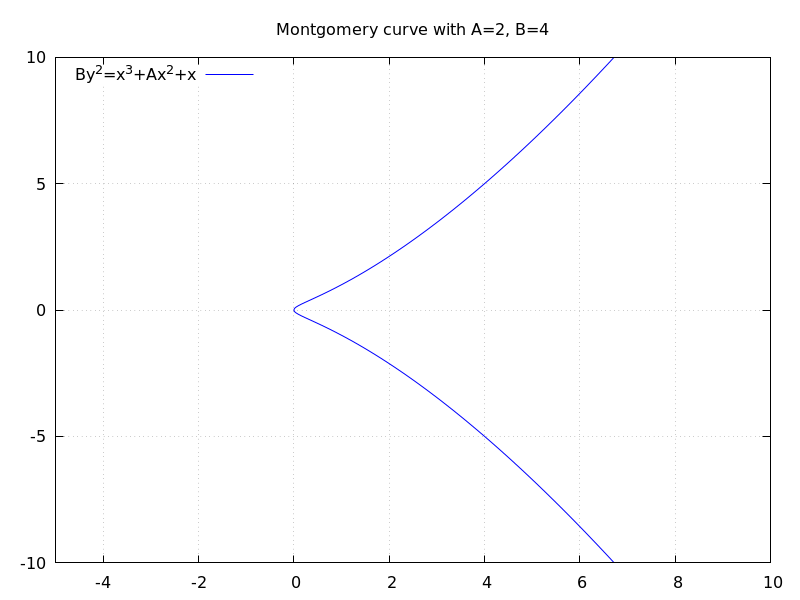
Picture 1: Montgomery curve $4y^2=x^3+2x^2+x$ in affine coordinates. As with (almost) any other elliptic curve, you can define rather simple algebra using the points of such elliptic curve. You define additions, doubling and scalar multiplications and of course, you can use it for some interesting cryptography. But it turns out that there are some problems with the efficiency of such algorithms in affine coordinates. Peter Montgomery[7] himself shown that using projective coordinates $X:Y:Z$ satisfying certain criteria allows us to perform the doubling and addition operations in more efficient way that is better suited for actual cryptography usage because of some interesting properties like constant-time duration for inputs of constant size. The criteria for projective coordinates is as follows: $$BY^Z=X^3+AX^Z+XZ^2$$ $$x=\frac{X}{Z}$$ $$y=\frac{Y}{Z}$$ Extending the codomain of the function to the $\mathbf{R}^3$ space yields some interesting curve stretched in the extra dimension as seen in Picture 2.

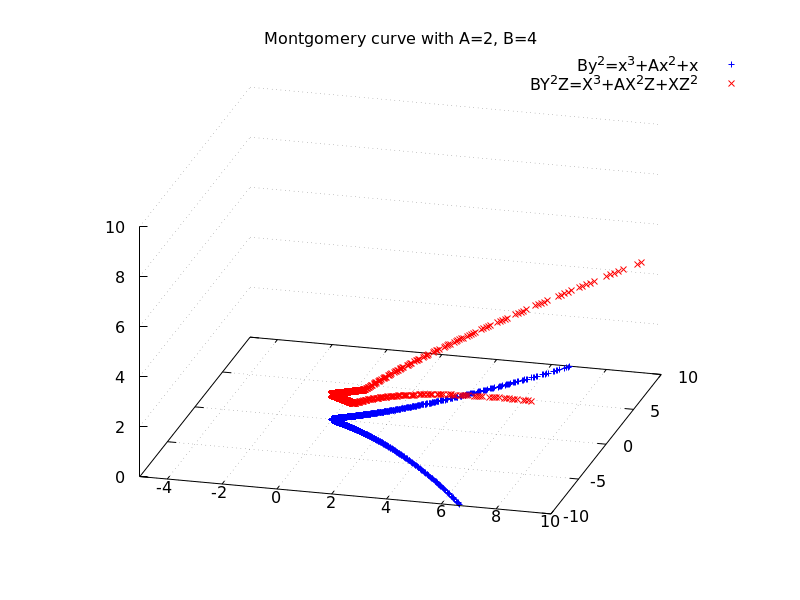
Picture 2: Comparison of the Montgomery curve in affine coordinates (blue, the bottom plane) and in projective coordinates (red, going up). Is is not only about the math - sometimes you really appreciate the visual part of the curve as well.

Hope you enjoyed our journey to one extra dimension and be prepared for more theory in the future! See you next Thursday.

References

1. Wikipedia contributors. (2020, January 8). Elliptic-curve cryptography. In Wikipedia, The Free Encyclopedia. Retrieved 17:00, February 4, 2020, from https://en.wikipedia.org/w/index.php?title=Elliptic-curve_cryptography&oldid=934813177

2. Wikipedia contributors. (2020, January 26). Elliptic curve. In Wikipedia, The Free Encyclopedia. Retrieved 17:01, February 4, 2020, from https://en.wikipedia.org/w/index.php?title=Elliptic_curve&oldid=937728084

3. https://trustica.cz/en/category/ecc/

4. Wikipedia contributors. (2020, January 28). Montgomery curve. In Wikipedia, The Free Encyclopedia. Retrieved 17:02, February 4, 2020, from https://en.wikipedia.org/w/index.php?title=Montgomery_curve&oldid=937969857

5. Wikipedia contributors. (2020, February 3). Affine space. In Wikipedia, The Free Encyclopedia. Retrieved 17:02, February 4, 2020, from https://en.wikipedia.org/w/index.php?title=Affine_space&oldid=938993782

6. Wikipedia contributors. (2019, December 18). Projective space. In Wikipedia, The Free Encyclopedia. Retrieved 17:03, February 4, 2020, from https://en.wikipedia.org/w/index.php?title=Projective_space&oldid=931344685

7. Wikipedia contributors. (2019, August 8). Peter Montgomery (mathematician). In Wikipedia, The Free Encyclopedia. Retrieved 17:02, February 4, 2020, from https://en.wikipedia.org/w/index.php?title=Peter_Montgomery_(mathematician)&oldid=909994855