Opcode Mask Pict

In previous post we have introduced a nice way to encode machine opcodes and their arguments as a bit mask. What about visualizing such opcodes? There surely is a way to include nice pictures to aid with reading the bit masks.

Just a quick recap of what the opcode mask looks like. It is an identifier starting with the colon : character and containing only numbers 0 and 1, lower- and upper-case letters a-z and A-Z, and padding characters - and _. Such identifier can easily be converted to a symbol and then processed.

For visualizing, we will convert the symbol to a string and strip the : prefix. That should give us all the information we need.

Firstly we convert the string to list of bit definitions. A simple procedure like the following one will suffice:

(define (make-bits s)
  (for/list ((ch (in-string s)))
    (case ch
      ((#\0) 0)
      ((#\1) 1)
      ((#\- #\_) #f)
      (else (string->symbol (make-string 1 ch))))))
(define sym ':1010-zccc-zzzz-zzzz)
(define str (substring (format "~a" sym) 1))
(make-bits str)

The result is:

'(1 0 1 0 #f z c c c #f z z z z #f z z z z)

It should be easy to make sense of this convention. The numerical constants 0 and 1 represent the constant bits of given opcode, the #f value represents spacing and the one-letter strings represent all the bits of given argument.

Secondly the bits need to be converted into an actual image. We will use the pict library to do so. A good approach is to start with creating a pict for single bit. The following procedure creates such pict. The #:pad argument specifies padding of the box, the #:border argument, if #t, creates a border around the box, the font size can be specified using the #:size argument and finally the #:guide argument should be used to pass on the widest element that will be present in the set of bits this box will be part of.

(define (bit-box c #:pad (pad 3) #:border (border #t) #:size (size 12) #:guide (guide ""))
  (define content
    (inset
     (text (format "~a" (or c "")) 'modern size)
     pad))
  (define back
    (ghost
     (inset
      (text (format "~a" guide) 'modern size)
      pad)))
  (cc-superimpose
   (rectangle (max (if c (pict-width back) 0) (pict-width content))
              (max (if c (pict-height back) 0) (pict-height content))
              #:border-color (if border "black" (make-color 0 0 0 0)))
   content))
(bit-box "z" #:guide "15")

The result is:

With this single-bit result, it is possible to start using pict combiners and create the whole bit-field pict. In that process a label for bit ordinal number is also added for clarity.

(define (make-bit-grid bits)
  (define lbits (label-bits bits))
  (define maxbit (apply max (filter number? (map cadr lbits))))
  (define bbits
    (for/list ((bit (in-list lbits)))
           (vc-append (bit-box (cadr bit) #:border (cadr bit) #:guide maxbit)
                      (bit-box (car bit) #:border (car bit) #:guide maxbit))))
  (define cbits
    (for/list ((bit (in-list lbits))
               (cell (in-list bbits)))
      (append bit (list (pict-width cell)))))
  (define wbits
    (for/fold ((res '())
               (l 0)
               #:result res)
              ((bit (in-list (reverse cbits))))
      (define w (+ l (caddr bit)))
      (values (cons (append bit (list w)) res) w)))
  (define pbits
  (apply hc-append
         (vc-append (bit-box "bit:" #:border #f)
                    (bit-box #f #:border #f))
         bbits))
  (values pbits wbits))
(define-values (pbits wbits) (make-bit-grid bits))

The result starts to resemble what we see in the original identifier:

The second value of the result will be used for aligning this image to other parts of the visualization. It is a list of lists containing the bit definition (as in the bits list), the ordinal bit number (we can see the big-endian representation here) or #f for spaces, then the width of given cell and as the last element the distance from the right edge of the combined image to the left edge of particular cell. It will soon become obvious why this is useful. The actual result for our sample identifier is:

'((1 15 20.0 338.0)
  (0 14 20.0 318.0)
  (1 13 20.0 298.0)
  (0 12 20.0 278.0)
  (#f #f 6 258.0)
  (z 11 20.0 252.0)
  (c 10 20.0 232.0)
  (c 9 20.0 212.0)
  (c 8 20.0 192.0)
  (#f #f 6 172.0)
  (z 7 20.0 166.0)
  (z 6 20.0 146.0)
  (z 5 20.0 126.0)
  (z 4 20.0 106.0)
  (#f #f 6 86.0)
  (z 3 20.0 80.0)
  (z 2 20.0 60.0)
  (z 1 20.0 40.0)
  (z 0 20.0 20.0))

Thirdly the bit group labels need to be extracted. A rather simple procedure will do:

(define (get-group-labels bits)
  (sort
   (set->list
    (for/set ((bit (in-list bits))
              #:when bit)
      (if (number? bit)
          #t
          bit)))
   (lambda (a b)
     (if (eq? a #t)
         #t
         (if (eq? b #t)
             #f
             (< (index-of bits a)
                (index-of bits b)))))))
(define glbls (get-group-labels bits))

And the result is just as follows:

'(#t z c)

The #t stands for the constant opcode bits and then the single-letter labels for the arguments. Notice that the list is in the order of first occurence of given element in the original identifier.

Afterwards we can start constructing the description lines. The code can be simplified but for now we stick to the good old if it ain't broken, don't fix it!

(define (make-group-descriptions labels wbits)
  (for/list ((lbl (in-list labels)))
    (define pred?
      (if (eq? lbl #t)
          number?
          (lambda (s)
            (eq? s lbl))))
    (list lbl
          (if (eq? lbl #t)
              "opcode"
              (format "~a" lbl))
          pred?
          (for/list ((bit (in-list wbits))
                     #:when (pred? (car bit)))
            (cadr bit)))))
(define gdescs (make-group-descriptions glbls wbits))

The result is a list of lists containing the bit label in the symbolic form (which is actually unused from now on) then the string representation to be shown, then a predicate for checking whether given bit definition belongs to this group, and a list of bit numbers which belong to this group label.

'((#t "opcode" #<procedure:number?> (15 14 13 12))
  (z "z" #<procedure:pred?> (11 7 6 5 4 3 2 1 0))
  (c "c" #<procedure:pred?> (10 9 8)))

This is great as it allows us to create a list of picts representing the labels easily:

(define (make-group-texts gdescs)
  (define longest
    (apply max (map (compose string-length cadr) gdescs)))
  (for/list ((gd (in-list gdescs)))
     (bit-box
      (format " ~a ~a- ~a bits"
              (cadr gd)
              (make-string (- longest (string-length (cadr gd))) #\space)
              (length (cadddr gd)))
      #:border #f)))
(define gtexts (make-group-texts gdescs))

As the result is a list of images, we will join them for displaying using a pict combinator vl-append:

(apply vl-append gtexts)

And we get this image:

The very next part is a bit tricky as we want to create connecting lines between the bit-field image and the combined label image. We start by defining a helper procedure which creates a mostly transparent pict of specified width and height which contains a set of lines, each coming from given bit matching the predicate (see the distances from the right edge above) going down almost to the bottom of the picture, taking a right turn to the right and going all the way to the right edge.

The line color and thickness is configurable to allow visually pleasing overlay of multiple such connectors.

(define (make-grid-connector-helper wbits pred? #:height (height 40) #:line-height (lheight 20) #:width (width 1) #:color (color "black"))
  (apply
   rc-superimpose
   (for/list ((bit (in-list wbits)))
     (cond ((pred? (car bit))
            (rb-superimpose
             (lt-superimpose
              (rectangle (cadddr bit) height #:border-color (make-color 0 0 0 0))
              (bvline (caddr bit) (- height (/ lheight 2)) width color))
             (hline (- (cadddr bit) (/ (caddr bit) 2)) lheight)))
           (else
            (blank))))))

Then the actual connector is what the helper generates in white color and with relatively thick lines over which the same image but in black and with relatively thin lines resides.

(define (make-grid-connector wbits pred? #:height (height 40) #:line-height (lheight 20))
  (cc-superimpose
   (make-grid-connector-helper wbits pred? #:height height #:line-height lheight #:width 5 #:color "white")
   (make-grid-connector-helper wbits pred? #:height height #:line-height lheight)))

(define (bvline w h t c)
  (cc-superimpose
   (blank w h)
   (filled-rectangle t h #:color c #:draw-border? #f)))

And using the connector pict maker a list of connector for all bit groups can be easily created:

(define (make-group-conns wbits gtexts gdescs)
  (define heights
    (for/fold ((res '())
               #:result (reverse res))
              ((gt (in-list gtexts)))
      (if (null? res)
          (list (pict-height gt))
          (cons (+ (pict-height gt)
                   (car res))
                res))))
  (for/list ((gt (in-list gtexts))
              (gd (in-list gdescs))
              (ht (in-list heights)))
    (make-grid-connector wbits (caddr gd) #:height ht #:line-height (pict-height gt))))
(define gconns (make-group-conns wbits gtexts gdescs))

Using yet-another pict combinator rt-superimpose we get the following image:

Finally we can put it all together to get a procedure that generates the whole pict from the symbol representing the original identifier:

(define (opcode-mask-pict s0)
  (define s (substring (format "~a" s0) 1))
  (define bits (make-bits s))
  (define-values (pbits wbits) (make-bit-grid bits))
  (define glbls (get-group-labels bits))
  (define gdescs (make-group-descriptions glbls wbits))
  (define gtexts (make-group-texts gdescs))
  (define gconns (make-group-conns wbits gtexts gdescs))
  (hb-append
   (vr-append
    pbits
    (apply rt-superimpose gconns))
   (apply vl-append gtexts)))
(opcode-mask-pict sym)

The final result should be self-explanatory:

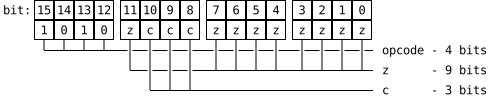
The generated image can be used directly when scribbling the documentation which is something we rely on heavily.

Hope you liked our venture down another rabbit-hole and see ya next time for more!